(최소 스패닝 트리)
# 문제
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
# 입력
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.
# 출력
첫째 줄에 최소 스패닝 트리의 가중치를 출력한다.
먼저 스패닝 트리가 무엇인지 알아보겠습니다!
신나는 나무
스패닝 트리는 다음 조건이 모두 충족되는 경우 트리입니다.
- 모든 노드가 연결되어 있습니다.
- 주기가 존재하지 않습니다.
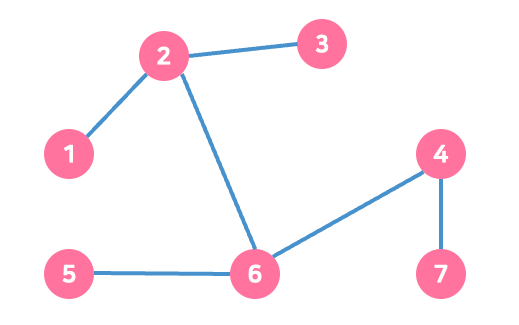
스패닝 트리의 올바른 예
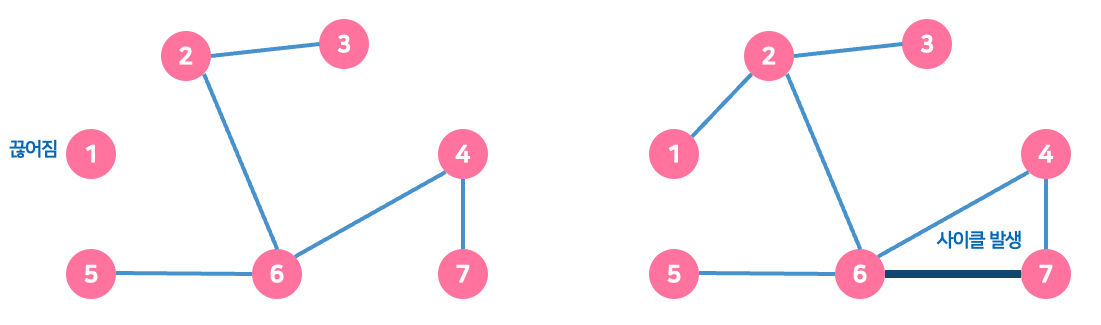
비신장 트리의 예
연결되지 않은 노드 또는 주기가 있는 경우 트리가 확장되지 않습니다.
최소 스패닝 트리 찾기
- 최소 스패닝 트리 알고리즘: 스패닝 트리 중 최소 비용빌드할 스패닝 트리를 찾는 알고리즘입니다.
최소한의 비용으로 스패닝 트리를 찾는 알고리즘, 크루스칼 알고리즘알아 보자!
크루스칼 알고리즘
- Kruskal 알고리즘은 대표적인 최소 스패닝 트리 알고리즘이다.
1) 모든 간선을 비용 오름차순으로 정렬한다.
2) 비용이 적은 간선을 가져온다.
3) 이 간선이 연결되면 사이클을 발생시키는지 확인한다.
4) 사이클을 발생시키지 않는다면, 이 간선을 신장 트리에 포함시킨다.
~반복~이는 항상 최적의 솔루션을 보장합니다.
1. 비용의 오름차순으로 모든 가장자리를 정렬합니다.
edges = () # 간선
for _ in range(E):
a, b, cost = map(int, sys.stdin.readline().split())
edges.append((cost, a, b))
edges.sort() # 비용순 오름차순 정렬
2. 유리한 이점을 얻으십시오.
- 1단계에서 오름차순으로 정렬해 놓았으니 하나씩 빼주시면 됩니다!
for edge in edges:
cost, a, b = edge # cost 오름차순으로 정렬되어 있음
3. 이 에지가 연결되면 주기가 발생하는지 확인하십시오.
이 에지가 연결될 때 순환을 일으키는지 확인하는 방법,
주어진 모서리의 모든 정점 상위 노드알아보는 것입니다
(각 노드의 부모를 찾아 두 부모가 같으면 그 가장자리가 연결될 때 순환을 일으킬 것입니다!!!)
왜,,주기가 뭐야,,,
연결된 노드가 같은 노드에 연결되면 뒤집어서 서로 만나는 것이 바로 싸이클~!
부모 노드는 각 노드입니다. 가장 작은 연결된 노드수단
이 부모 노드가 동일한 노드를 연결하면 주기가 발생합니다.
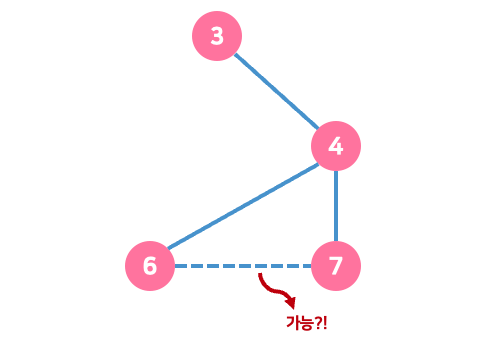
위 그림에서 점선으로 표시된 부분입니다. 6-7가장자리가 연결될 때 주기가 발생합니까?
- 7에 연결된 가장 작은 노드는 3이고,
- 6에 연결된 가장 작은 노드는 3입니다.
둘 다 3으로 이어집니다. 다시 말해서, 6-7 에지가 연결되면 주기가 트리거됩니다.
그럴땐 연결하면 안됩니다. 싸이클이 발생하면 스패닝 트리가 아닙니다~!
이제 부모 노드를 먼저 찾아야 합니다.
2-1) 부모 테이블을 생성합니다.
- 인덱스를 노드로 설정하고 값을 부모 노드로 설정합니다.
parent(노드) = 부모노드 - 노드는 1부터 지정되므로 상위 테이블의 크기는 노드 수 + 1입니다.
(인덱스 0을 사용하지 않기 때문입니다!) - 먼저 자체적으로 초기화합니다.
(노드 1 부모는 1, 노드 2 부모는 2…)
# 부모를 담을 테이블 (parent(노드) = 부모노드)
parent = (0) * (V + 1)
# 부모를 자기 자신으로 초기화
for i in range(1, V+1):
parent(i) = i
2-2) 부모 노드가 동일한지 확인합니다.
이것은 두 번째 for 문으로 이어집니다.
- 비용이 가장 낮은 에지를 선택하고 해당 에지에 연결된 모든 노드에 동일한 부모 노드가 있는지 확인합니다.
(같은 부모는 같은 집합에 속하는 것을 의미합니다. 같은 집합에 속할 필요는 없습니다.)
for edge in edges:
cost, a, b = edge # cost 오름차순으로 정렬되어 있음
if find_parent(a) != find_parent(b): # 같은 집합이 아니면,
- 아래는 부모를 찾는 기능입니다.
함수를 재귀적으로 호출하고 부모 테이블의 값을 즉시 업데이트(경로 압축 기술)하여 시간 복잡도를 개선했습니다.
# 부모 찾는 함수
def find_parent(x):
if parent(x) != x:
parent(x) = find_parent(parent(x))
return parent(x)
4. 주기가 발생하지 않으면 스패닝 트리에 에지를 포함합니다.
2 또는 3은 지침을 따릅니다.
result = 0
for edge in edges:
cost, a, b = edge # cost 오름차순으로 정렬되어 있음
if find_parent(a) != find_parent(b): # 같은 집합이 아니면,
union_parent(a, b) # 연결
result += cost # 연결된 것 cost 누적- 비용 절감을 위한 변수
result새로 선언했습니다. - 에지가 연결될 때마다 해당 에지의 비용은
result이 값을 최종 결과로 출력합니다. - 실제로 트렁크를 연결하는 부분
union_parent(a, b)이 함수 안에서 발생합니다.
스패닝 트리에 에지를 포함하는 기능
union_parent(a, b) 함수에 무엇이 있는지 봅시다!
def union_parent(a, b):
# 집합(부모 노드) 찾기
a = find_parent(a)
b = find_parent(b)
# 큰 거에서 작은 거로 연결
if a < b:
parent(b) = a
else:
parent(a) = b연결할 두 노드의 부모를 찾아 연결합니다.
왜?

- 노드를 연결할 때 방향은 큰 노드에서 작은 노드로 향해야 하며 작은 노드가 큰 노드의 부모가 됩니다.
즉, 노드를 연결하려면 큰 노드의 부모 노드를 작은 노드 위에 놓으세요!! - 그런데,,,,
노드 3과 노드 2가 연결되면,
노드 2가 1에 연결되어 있으므로
노드 3의 부모 노드도 2가 아닌 1이 됩니다. - 따라서 Edge가 연결될 때마다 상위 노드 업데이트그것을해야합니다!
3과 2를 결합할 때 3 -> 2로 끝나는 것이 아니라 2의 부모를 찾아 3과 결합하여 3 -> 1로 변경해야 합니다!! - 부모노드를 연결하기 때문에 함수는 먼저 부모노드를 찾는다.
find_parent호출하여 찾은
큰 부모 노드를 작은 부모 노드에 연결합니다. 즉, 부모 노드를 함께 연결합니다.
Self와 parent는 당연히 연결되어 있기 때문에 부모 노드만 연결하면 연결이 계속됩니다. - 이와 같이 연결되지 않은 것 중 가장 저렴한 것을 한두 개 추가하여 한 번에 하나씩 연결하여 최소 스패닝 트리를 완성한다.
끝!
전체 코드
import sys
V, E = map(int, input().split()) # 정점의 개수, 간선의 개수
# 부모를 담을 테이블 (parent(노드) = 부모노드)
parent = (0) * (V + 1)
# 부모를 자기 자신으로 초기화
for i in range(1, V+1):
parent(i) = i
# 부모 찾는 함수
def find_parent(x):
if parent(x) != x:
parent(x) = find_parent(parent(x))
return parent(x)
# 간선 연결하는 함수(집합 합치기)
def union_parent(a, b):
# 집합(부모 노드) 찾기
a = find_parent(a)
b = find_parent(b)
# 큰 거에서 작은 거로 연결
if a < b:
parent(b) = a
else:
parent(a) = b
edges = () # 간선
for _ in range(E):
a, b, cost = map(int, sys.stdin.readline().split())
edges.append((cost, a, b))
edges.sort() # 비용순 오름차순 정렬
result = 0
for edge in edges:
cost, a, b = edge # cost 오름차순으로 정렬되어 있음
if find_parent(a) != find_parent(b): # 같은 집합이 아니면,
union_parent(a, b) # 연결
result += cost # 연결된 것 cost 누적
print(result)