4-6 로지스틱 회귀 뉴런을 갖는 단층 신경망의 구조
– 일반 신경망
입력층, 은닉층, 출력층
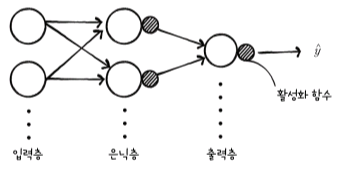
– 단층 신경망

– 확률적 경사하강법, 배치 경사하강법
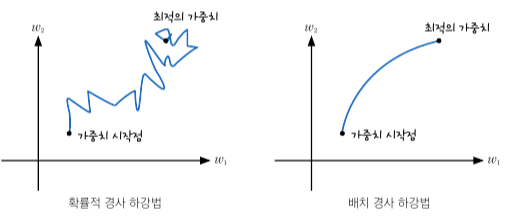
– 단층 신경망 클래스
class SingleLayer:
def __init__(self):
self.w = None
self.b = None
self.losses = ()
def forpass(self, x):
z = np.sum(x * self.w) + self.b # 직선 방정식 계산
return z
def backprop(self, x ,err):
w_grad = x *err # 가중치에 대한 그레이디언트 계산
b_grad = 1 *err # 절편에 대한 그레이디언트 계산
return w_grad, b_grad
def activation(self, z):
z = np.clip(z, -100, None) # 안전한 np.exp() 계산을 위해
a = 1 / (1 + np.exp(-z)) # 시그모이드 계산
return a
def fit(self, x ,y, epochs=100):
self.w = np.ones(x.shape(1)) # 가중치 초기화
self.b = 0 # 절편 초기화
for i in range(epochs): # epochs만큼 반복
loss = 0
indexes = np.random.permutation(np.arange(len(x))) # 인덱스 섞기
for i in indexes: # 모든 샘플에 대해 반복
z = self.forpass(x(i)) # 정방향 계산
a = self.activation(z) # 활성화 함수 적용
err = -(y(i) - a) # 오차 계산
w_grad, b_grad = self.backprop(x(i), err) # 역방향 계산
self.w -= w_grad # 가중치 업데이트
self.b -= b_grad # 절편 업데이트
a = np.clip(a, 1e-10, 1-1e-10) # 안전한 로그 계산을 위해 클리핑한 후 손실 누적
loss += -(y(i)*np.log(a)+(1-y(i))*np.log(1-a)) # 에포크마다 평균 손실 저정
self.losses.append(loss/len(y))
def predict(self, x):
z = (self.forpass(x_i) for x_i in x) # 선형 함수 적용
return np.array(z) > 0 # 계단 함수 적용
def score(self, x, y):
return np.mean(self.predict(x) == y)– 단층 신경망 훈련
1. 단층 신경망 훈련 및 출력 정확도
layer = SingleLayer()
layer.fit(x_train, y_train)
layer.score(x_test, y_test)
##출력: 0.9298245614035088
2. 손실함수 누적값 확인
plt.plot(layer.losses)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

반응형
4-7 scikit learn으로 로지스틱 회귀 수행
– Scikit Learn으로 경사하강법 적용
1. 로지스틱 손실 함수 부여
from sklearn.linear_model import SGDClassifier
sgd = SGDClassifier(loss="log", max_iter = 100, tol=1e-3, random_state = 42)
2, scikit-learn으로 학습 및 평가
sgd.fit(x_train, y_train)
sgd.score(x_test, y_test)
##출력: 0.8333333333333334
3. scikit learn을 사용한 예측
sgd.predict(x_test(0:10))
##출력: array((0, 1, 0, 0, 0, 0, 1, 0, 0, 0))
※ 내용